STL关联式容器分为set和map两大类,以及这两大类的衍生体multiset和multimap,这些容器的底层机制均为rb-tree。rb-tree也是一个独立容器,但并不开放给外界使用。SGI STL还提供了一个不在标准规格之列的关联式容器hash table,以及以此hashtable为底层机制的hash_set,hash_map,hash_miltimap和hash_multiset.
关联式容器,每笔数据都有一个键值(key)和一个实值(value),当元素被插入到关联式容器中时,容器内部结构便依照其键值大小,以某种特定规则将这个元素放置于适当位置。set的键值就是实值,map的键值可以和实值分开,并形成一种映射关系,所以map被称为映射表。关联式容器没有所谓头尾(只有最大值和最小值),所以不提供push_back(),push_front(),end()等操作行为。
关联式容器的内部是一个平衡二叉树,平衡二叉树有很多种类型:AVL-tree, RB-tree,AA-tree(RB-tree的变体),在STL中使用的是RB-tree。
树
根节点至任何节点之间有唯一路径,路径所经过的边数,称为路径长度。根节点至任何节点的路径长度,即该节点的深度。根节点的深度是0.某节点至其最深子节点(叶节点)的路径长度,称为该节点的高度。任何节点的大小是指其所有子代(包括自己)的节点总数。
二叉搜索树
二叉搜索树的设计原则是:任何节点的键值一定大于其左子树中的每一个节点的键值,并小于其右子树中的每一个节点的键值。
平衡二叉搜索树
可能因为输入值不够随机,或者某些插入和删除操作,二叉搜索树可能会失去平衡,造成搜索效率低下的情况。
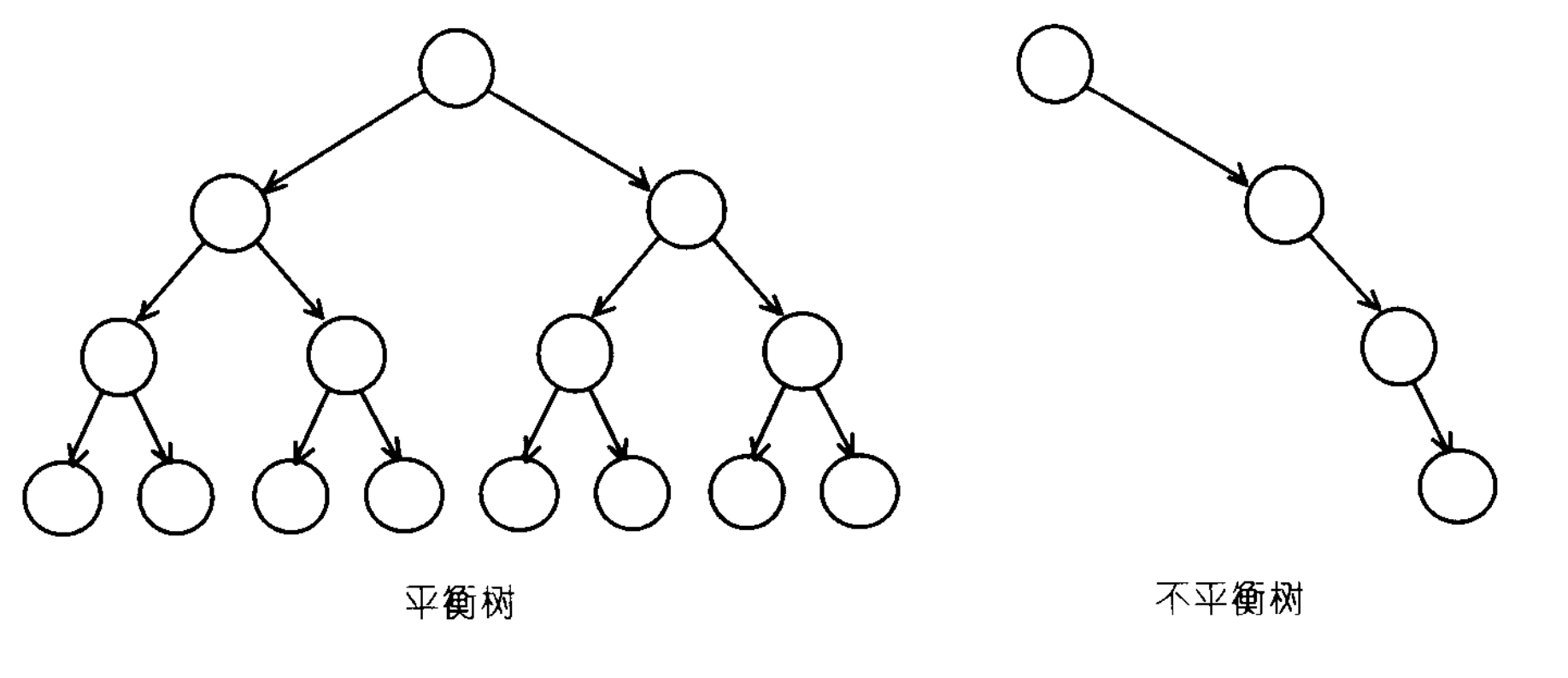
树的平衡,没有一个绝对的测量标准。大致意义是:没有任何一个节点过深。不同的平衡条件,造就出不同的效率表现,以及不同的实现复杂度。
AVL tree(Adelson-Velskii-Landis tree)
有额外平衡条件(任何节点的左右子树的高度相差不超过1)的二叉搜索树,确保二叉树的高度为O(logN),保证对数深度平衡状态。
实现
节点的定义
template<class K, class V>
struct AVLTreeNode{
pair<K,V> _kv; //存储键值对,键为值的索引用于比较
int _bf; //平衡因子
AVLTreeNode* _left; //左孩子节点
AVLTreeNode* _right; //右孩子节点
AVLTreeNode* _parent; //父节点
AVLTreeNode(const pair<K,V>& val = pair<K,V>()):_kv(val), _bf(0), left(nullptr), _right(nullptr), _parent(nullptr){} //默认构造函数
};
新节点插入操作
在新节点插入时,和普通二叉搜索树的插入规则一致(小于根节点,置于根节点的左子树;大于根节点,置于根节点的右子树)。
template<class K, class V>
bool insert(const pair<K,V>& kv){
if(_root == nullptr){ //树为空,则插入进来的节点为根节点
_root = new AVLTreeNode(kv);
return true;
}
AVLTreeNode* parent = nullptr;
AVLTreeNode* cur = _root;
while(cur){
if (cur->_kv.first > kv.first){ //小于当前节点
parent = cur;
cur = cur->_left;
}
else if (cur->_kv.first < kv.first){ //大于当前节点
parent = cur;
cur = cur->_right;
}
else{ //存在该节点,则退出
return false;
}
}
cur = new AVLTreeNode(kv);
if (parent->_kv.first < kv.first){
parent->_right = cur;
}
else{
parent->_left = cur;
}
cur->_parent = praent;
//判断插入之后是否导致不平衡
}
但是,插入某节点后,AVL tree的平衡可能被破坏,分为两种情况:
- 外侧插入
- 该插入节点E位于A的左节点的左子树
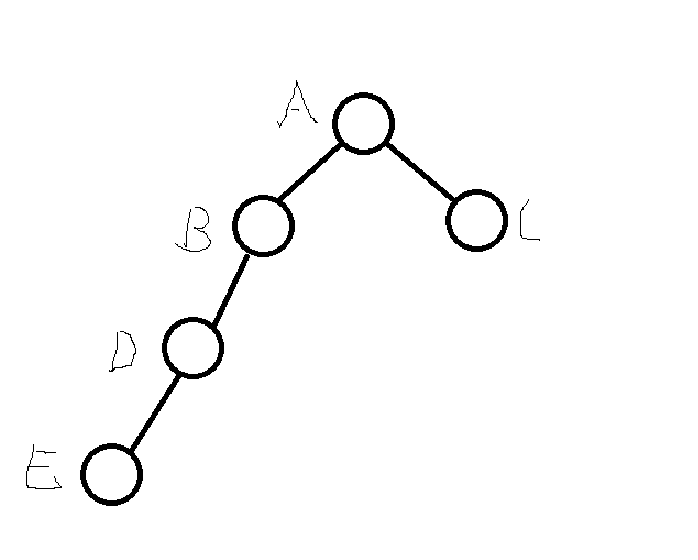
-
该插入节点E位于A的右节点的右子树
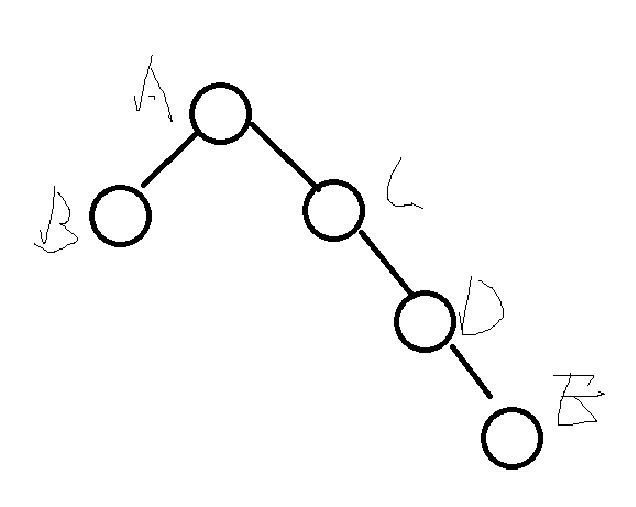
- 内侧插入
-
该插入节点F位于A的右节点的左子树
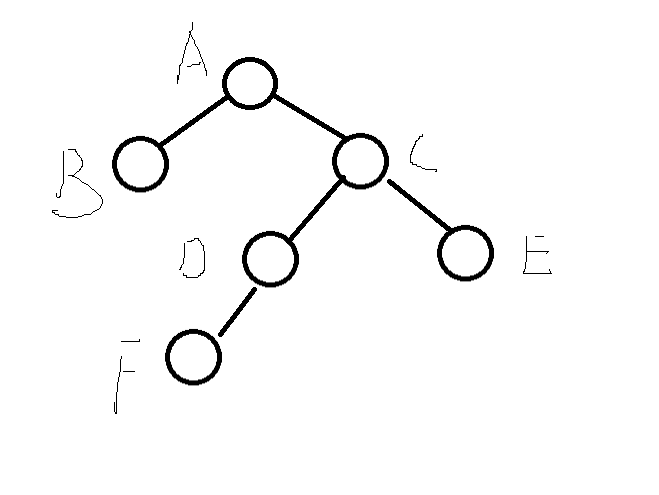
-
该插入节点F位于A的左节点的右子树
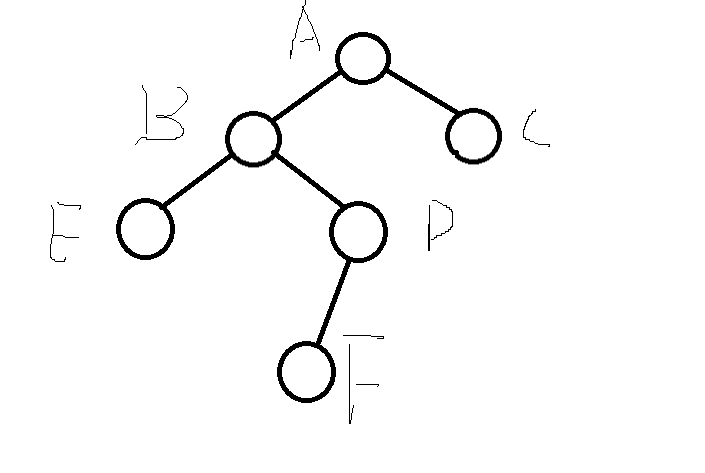
情况1需要单旋
- 节点A作为根节点的树中,左子树比右子树高的多,我们需要把右子树变高,还要保持二叉搜索树的性质(右大于左)。只能把根节点A移下去作为右子树的一部分,根节点的左孩子B移上去作为根节点。这是A节点(大于B)就必须为B的右子树,B原本的右子树(大于B小于A)可以为A的左子树。也称为右旋(对于节点A来说就是向右旋转)。
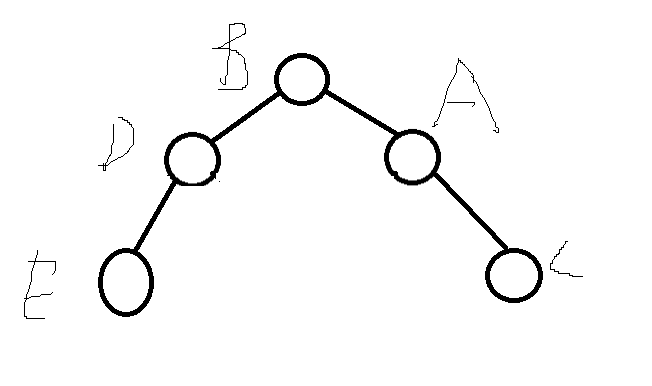
- 左旋同理,只不过调整了指向。
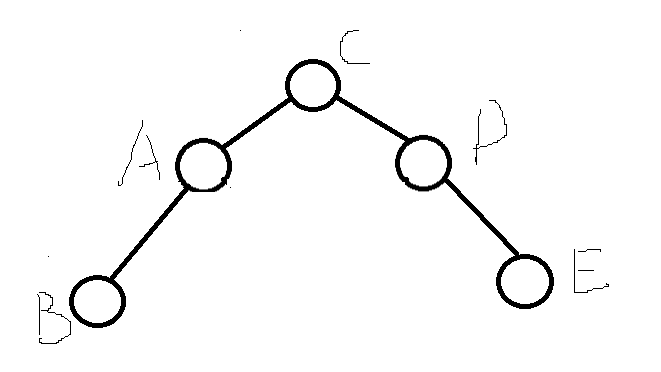
情况2需要双旋
- 依然是需要把根节点A移下去作为左子树的一部分,但是不能对节点C进行左旋。因为节点C有左孩子,左旋结束后,节点A只能为节点C左孩子的孩子,这样又会导致不平衡。节点F位于A的右节点的左子树,故A的右节点的左子树较高,我们可以直接选取节点D为整棵树的根节点,节点A必须为节点D的左孩子,节点D原本的左孩子为节点A的右孩子;节点C必须为节点D的右孩子,节点D原本的右孩子为节点D的左孩子。
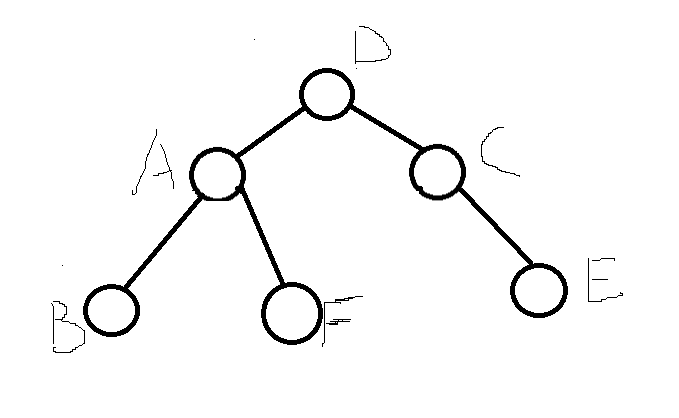
可以分为两个步骤,先把节点C右旋,再把节点A左旋。
- 与上述类似,只不过调整了指向。
右单旋
void RotateR(AVLTreeNode* parent){ //传入A节点
AVLTreeNode* subL = parent->_left; //得到B节点
AVLTreeNode* subLR = subL->_right; //得到B的右孩子
//旋转过程
parent->_left = subLR; //B的右孩子变为A的左孩子
if(subLR){ //若B的右孩子不为空,则必须改变父节点指向
subLR->_parent = parent;
}
AVLTreeNode* ppNode = parent->_parent; //得到节点A的父节点
subL->_right = parent; //B节点的右孩子指向A
parent->_parent = subL; //改变A节点的父节点指向
if(ppNode){ //节点A只是这个子树的根节点,他还有父节点
if(parent = ppnode->_left){
ppnode->_left = subL;
}else{
ppnode->_right = subL;
}
subL->_parent = ppNode;
}else{ //节点A为整棵树的根节点,父节点为空
root = subL; //设置节点B为整棵树的根节点
subL->_parent = nullptr;
}
//调整平衡因子,因为只有A和B的相对位置发生改变
subL->_bf = parent->_bf = 0;
}
左单旋
void RotateL(AVLTreeNode* parent){
AVLTreeNode* subR = parent->_right;
AVLTreeNode* subRL = subR->_left;
parent->_right = subRL;
if (subRL){
subRL->_parent = parent;
}
AVLTreeNode* ppNode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (ppNode){
if (parent == ppNode->_left){
ppNode->_left = subR;
}else{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}else{
_root = subR;
subR->_parent = nullptr;
}
subR->_bf = parent->_bf = 0;
}
右左双旋
根据我们的分析,双旋需要进行3个节点(D,C,A)相对位置的变动,我们需要调节这个三个节点的平衡因子。由于第一次旋转时,D和C的状况有多种,就对应了调整后多种不同的平衡因子(右子树高度-左子树高度)情况:
- 当B,E,F都不存在,这时D为新插入的节点,D的bf为0,C的为-1,A的为2.调整之后,都为0.
- 当为上述图中的情况,F为新插入的节点,D的bf为-1,C的为-1,A的为-1,调整之后,D的bf为0,A为0,C为1
- 当F为D的右孩子时,F为新插入的节点,D的bf为1,C的为-1,A的为-1,调整之后,D的bf为0,A为-1,C为0
为什么以D节点为标准呢?因为每次旋转都要安置D的左右孩子,这样就会引起其他两个节点的平衡因子变化。
void RotateRL(AVLTreeNode* parent){ //传入A节点
AVLTreeNode* subR = parent->_right; //得到C节点
AVLTreeNode* subRL = subR->_left; //得到D节点
int bf = subR->_bf; //得到D的bf
//双旋
RotateR(subR); //对C右旋
RotateL(parent); //对A左旋
//调整平衡因子
if (bf == 0){
parent->_bf = 0;
subRL->_bf = 0;
subR->_bf = 0;
}
else if (bf == -1){
parent->_bf = 0;
subR->_bf = 1;
subRL->_bf = 0;
}
else if (bf == 1){
parent->_bf = -1;
subR->_bf = 0;
subRL->_bf = 0;
}
}
左右双旋
void RotateLR(AVLTreeNode* parent){
AVLTreeNode* subL = parent->_left;
AVLTreeNode* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == 0){
parent->_bf = 0;
subL->_bf = 0;
subLR->_bf = 0;
}
else if (bf == -1){
parent->_bf = 1;
subL->_bf = 0;
subLR->_bf = 0;
}
else if (bf == 1){
parent->_bf = 0;
subL->_bf = -1;
subLR->_bf = 0;
}
}
接下来的insert函数
template<class K, class V>
bool insert(const pair<K,V>& kv){
//...
//判断插入之后是否导致不平衡,不平衡则旋转
while(parent){
if(cur == parent->_left){ //父节点的左子树高度加1,平衡因子减一
parent->bf--;
}else{
parent->bf++;
}
if(parent->_bf == 0){ //父节点的平衡因子由原来的-1/1变为0,总体高度不变,只是给高度较小的子树的高度加1.对总体的平衡因子也没有影响
break;
}else if(parent->_bf == 1 || parent->_bf == -1){ //原本父节点的左右子树高度是相同的,插入该节点后,改变了以父节点为根节点的子树的高度,可能会影响整棵树,需要向上遍历父节点
cur = parent;
parent = parent->_parent;
}else if(parent->_bf == -2 || parent->_bf == 2){
//这时的cur不再是插入的节点,而是对应的节点B
if(parent->_bf == -2 && cur->_bf == -1){
RotateR(parent);
}else if(parent->_bf == 2 && cur->_bf == 1){
RotateL(parent);
}else if(parent->_bf == 2 && cur->_bf == -1){
RotateRL(parent);
}else if(parent->_bf == -2 && cur->_bf == 1){
RotateLR(parent);
}
//该处调整后,所有的都满足条件,可以数学证明
break;
}
}
return true;
}
删除操作
和普通二叉搜索树的删除流程一样,但是删除之后需要检测平衡因子,若不满足条件,则调整。
删除的节点分为三种情况:
- 叶子节点,直接删除
- 只有一个孩子节点,删除该节点,该节点的父节点指向其孩子节点
- 有两个孩子节点,找到待删除节点的前驱或后继节点(叶子节点),替换值,就转换为删除找到的节点。在这里要进行一步特殊处理,需要判断该节点的哪个子树比较高,若左子树高,则找前驱节点;否则,找后继节点。这样处理后,删除前驱或后继节点后,不会导致以原删除节点为根的树的平衡因子的改变。
delete函数
AVLTreeNode* _remove(AVLTreeNode* node, const K& val){ //传入根节点和待删除节点的索引key
if(node == nullptr){
return nullptr;
}
if(node->_kv.first > val){ //该节点位于根节点的左子树
node->_left = _remove(node->_left, val); //删除该节点
node->_bf = Depth(node->_right) - Depth(node->_left); //调整平衡因子,原文放在倒数第二行
//判断平衡因子,决定是否旋转(可以对比插入操作)
if(abs(node->_bf) > 1){
if(Depth(node->_right->_right) >= Depth(node->_right->_left)){ //右孩子的右子树高
RotateL(node);
}else{ //右孩子的左子树高
RotateRL(node);
}
}
}else if(node->_kv.first < val){
node->_right = _remove(node->_right, val); //删除该节点
//判断平衡因子,决定是否旋转(可以对比插入操作)
if(abs(node->_bf) > 1){
if(Depth(node->_left->_left) >= Depth(node->_left->_right)){ //左孩子的左子树高
RotateR(node);
}else{ //左孩子的右子树高
RotateLR(node);
}
}
}else{ //定位到删除节点
if(node->_left != nullptr && node->_right != nullptr){ //有两个孩子
if(Depth(node->_left) >= Depth(node->_right)){ //判断哪棵树更高
AVLTreeNode* prev = node->_left;
while (prev->_right)
prev = prev->_right; //定位到前驱节点
node->_kv.val = prev->_kv.val; //原文是first
node->_left = _remove(node->_left, prev->_kv.first); //转为删除前驱节点
}else{
AVLTreeNode* post = node->_right;
while (post->_left)
post = post->_left;
node->_kv.val = prev->_kv.val;
node->right = _remove(node->_right, post->_kv.first);
}
}else{ //只有一个孩子节点或者没有孩子节点
if(node->_left != nullptr){ //直接删除该节点,返回孩子节点
AVLTreeNode* left = node->_left;
delete node;
return left;
}else if(node->_right != nullptr){
AVLTreeNode* right = node->_right;
delete node;
return right;
}else{
return nullptr;
}
}
}
//node->_bf = Depth(node->_right) - Depth(node->_left);
return node;
}
AVL tree查询非常有效率,但是插入和删除操作时需要进行很多复杂的操作维持树的平衡,所以对于不经常变动的数据可以使用该结构。