题目
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例1:
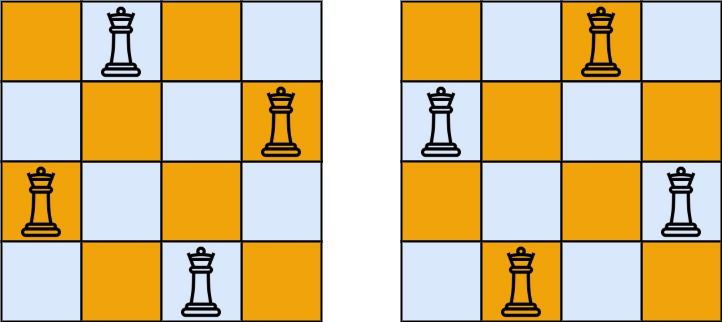
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[["Q"]]
思路
我没放弃这个题哦~
根据n创建一个二维数组,作为是否可以使用的位置,关键在于确定每个皇后斜列的对应位置和皇后的位置关系,从而改变二维数组的值
class Solution {
public:
vector<vector<string>> res;
vector<string> path;
void update_used(vector<vector<bool>>& unsafe_index, int i, int j, int n)
{
int row = i;
int column = j;
//每列的行位置不用改变
//每行的列位置改变
for(int k = row + 1; k < n; ++k) unsafe_index[k][j] = true;
//左斜边位置改变
while(true)
{
if(row == n-1 || column == 0) break;
unsafe_index[++row][--column] = true;
}
row = i;
column = j;
//右斜边位置改变
while(true)
{
if(row == n-1 || column == n-1) break;
unsafe_index[++row][++column] = true;
}
}
void solveNQueensAux(int n, vector<vector<bool>> unsafe_index, int iter)
{
if(iter == n) return;
for(int j = 0; j < n; ++j)
{
vector<vector<bool>> unsafe_index_tmp = unsafe_index;
if(unsafe_index_tmp[iter][j]) continue;
string queen_index_path = string(n, '.');
queen_index_path[j] = 'Q';
path.emplace_back(queen_index_path);
if(path.size() == n)
{
res.emplace_back(path);
}
else
{
update_used(unsafe_index_tmp, iter, j, n);
solveNQueensAux(n, unsafe_index_tmp, iter + 1);
}
path.pop_back();
}
}
vector<vector<string>> solveNQueens(int n) {
vector<vector<bool>> unsafe_index(n, vector<bool>(n, false));
solveNQueensAux(n, unsafe_index, 0);
return res;
}
};
一个小时十五分钟win
虽然时间只超过了5.07%的用户